Superdense Coding
In the classical realm, if you transmit the single bit, you can encode exactly two values: zero or one.
In the quantum realm, you can transmit the single qubit, but encode two bits, i.e. four values. To do this you can use quantum entanglement: you share an EPR pair between participants before the transmission and consume it during the transmission.
 Create EPR pair
Create EPR pair
Generate an EPR pair: the state \(\frac{1}{\sqrt{2}} \big( |00\rangle + |11\rangle \big)\).
To the top
 Encode two bits
Encode two bits
Alice and Bob each received their part of the EPR pair, i.e. the state \(\frac{1}{\sqrt{2}} \big( |00\rangle + |11\rangle \big)\). Alice wants to encode two bits using her component. She applies some operations (that depend on her bits) to her qubit. Implement this transformation.
Variants:
- \(\frac{1}{\sqrt{2}} \big( |00\rangle + |11\rangle \big)\)
- \(\frac{1}{\sqrt{2}} \big( |01\rangle + |10\rangle \big)\)
- \(\frac{1}{\sqrt{2}} \big( |00\rangle - |11\rangle \big)\)
- \(\frac{1}{\sqrt{2}} \big( |01\rangle - |10\rangle \big)\)
Your variant:
You can apply operations only to the first qubit!
To the top
 Decode bits
Decode bits
After encoding, Alice sends her qubit to Bob. Now Bob has to recover Alice's bits.
What Bob wants to get:
- \(\frac{1}{\sqrt{2}} \big( |00\rangle + |11\rangle \big) \mapsto |00\rangle\)
- \(\frac{1}{\sqrt{2}} \big( |01\rangle + |10\rangle \big) \mapsto |01\rangle\)
- \(\frac{1}{\sqrt{2}} \big( |00\rangle - |11\rangle \big) \mapsto |10\rangle\)
- \(\frac{1}{\sqrt{2}} \big( |01\rangle - |10\rangle \big) \mapsto |11\rangle\)
You don't know exactly, which state is yours, but after applying the operations you should get the results shown above.
To the top
Help: how to use the system?
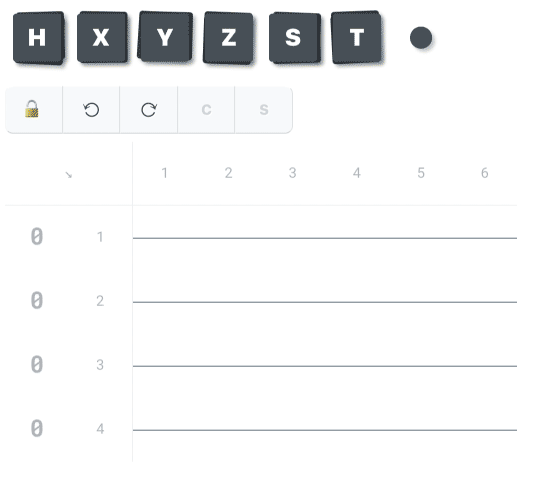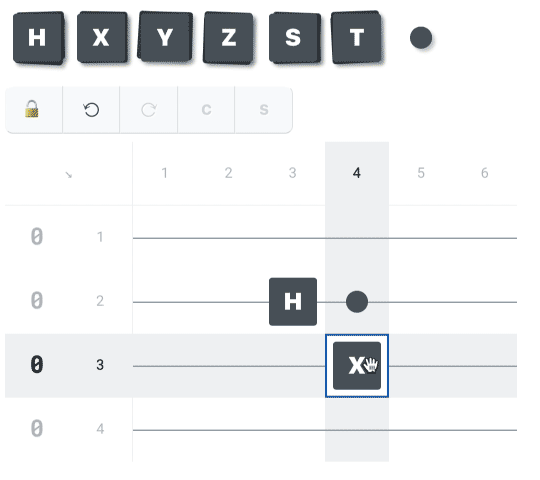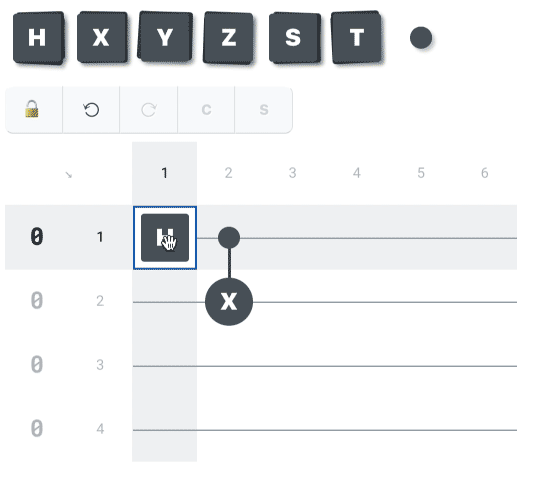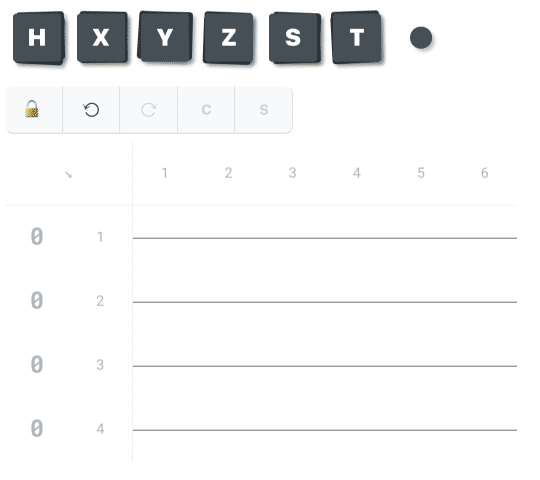
To the top